Definition

A quotient filter is a probabilistic data structure used for efficient set membership testing. It is similar to a Bloom filter, but it provides exact false positive rates and can also support deletions.

The basic idea behind a quotient filter is to divide a large hash table into a fixed number of small, equally sized cells. Each cell contains a quotient and a remainder value, which are calculated from the hash of the inserted element. The quotient value determines the cell in which the element is stored, and the remainder value is used to resolve collisions.

To check if an element is in the filter, its hash is used to calculate the quotient and remainder values. The filter then checks the corresponding cell for the quotient value, and if it matches, it checks the remainder value to determine if the element is present.

The false positive rate of a quotient filter can be adjusted by changing the number of cells and the number of bits used to represent the quotient and remainder values. A higher number of cells or bits results in a lower false positive rate, but also increases the storage requirements of the filter.

Quotient filters have several advantages over Bloom filters, including exact false positive rates, support for deletions, and a lower memory overhead for equivalent false positive rates. However, they can be slower than Bloom filters due to the need to calculate the quotient and remainder values for each lookup.

Implementation

The data structure is essentially a wrapper around vec of slots. A slot is just unsigned integer number which represents remainder and a metadata which is just u8. I used remainder u64 because most of the hashes produces an 64 bit result. However, while accessing this vector of slots, u32 or u16 would be a better idea, due to length of cache line is 64 bit. Because of this, I created a generic one, and copy pasted 16-32 bit ones.

struct Slot {
    remainder: u64,
    metadata: u8
}

struct QuotientFilter {
    table_size: usize,
    table: Vec<Slot>
}

While initializing the Quotient filter, we only provide the size of quotient. If it’s 2, then the table size becomes 2^2 = 4. For remainder we only use 62 right-most bits only out of 64. The quotient bits are used for indexing. 00, 01, 10, 11, respectivelly.

Metadata

It’s originally just 3 bits, but I used another bit deleted slots. So 4 bits. Then why u8? There isn’t a type that represents a bit. We can’t avoid wasting 4 bits, the minimum type is a byte, u8.

So the metadata have 4 bits. Because we care about bits only, we do many bitwise operations.

• is_shifted: is the slot in its original spot?
• run_continued: is the slot continueation of a run?
• bucket_occupied: is any quotient hashed to this slot?
• tombstone: is deleted?

A run is, one or more slots, hashed into the same slot. A cluster is one or more runs. These definitions and metadata helps us to deal with insertion, deletion, shifting and almost everything else.

Insertion

This is the heart of a quotient filter. The other parts are easy, if you get this place correct. Because you have to do the shifting right. I mean what would you do, if multiple hash results showing the same quotient? There were some edge-cases, the more I solved, the more the code become cumbersome. The algorithm is like this

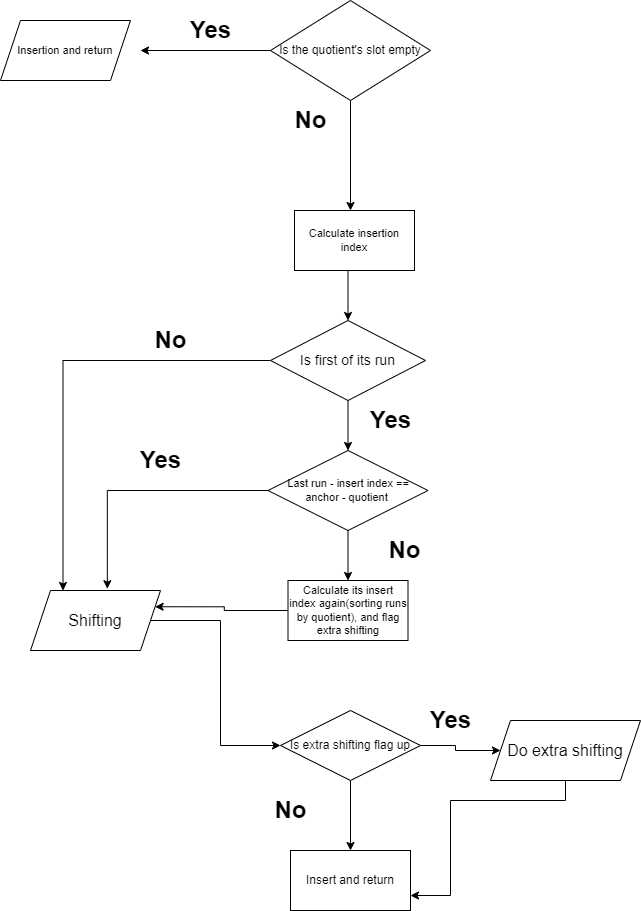
The problem arises when you want to reconstruct fingerprints(the hash result) that got used to insert, quotient and remainder combined. I solved the problems with extra shifting, which is if there are multiple runs, sorting runs based on their quotients. After that, you’re able to know which run have the which quotient. If you don’t do that, you still can handle quotient filter, however you can’t resize and merge.

Result

I published my final code with a crate named ‘quotient-filter’, the source code is open here.

More

To learn quotient filter, you can check this blog post, and you can read this book.